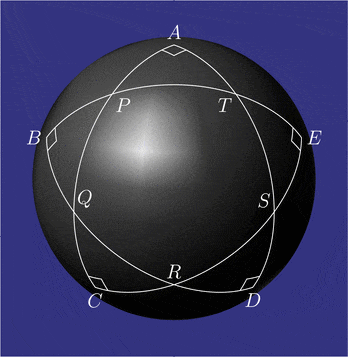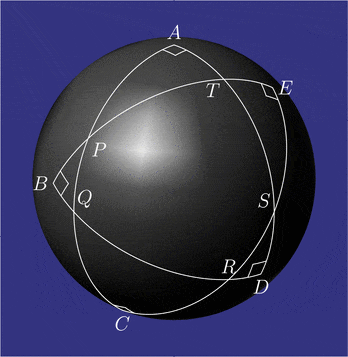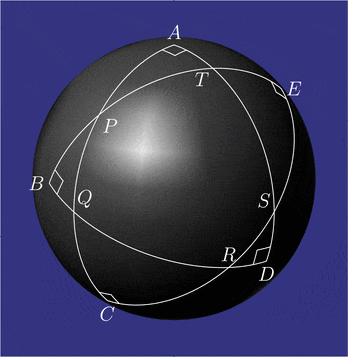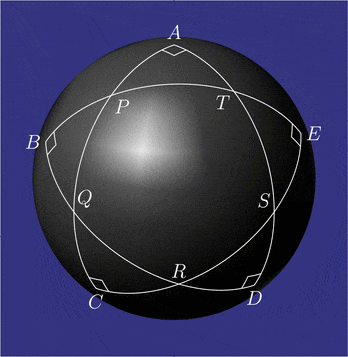
Przykładowe konfiguracje pentagramma mirificum Zależności między kątami i bokami pięciu trójkątów prostokątnych przyległych do wewnętrznego pięciokąta: ich koła Nepera zawierają przesunięte cyklicznie części
(
a
,
{\displaystyle (a,}
π
/
2
−
B
,
{\displaystyle \pi /2-B,}
π
/
2
−
c
,
{\displaystyle \pi /2-c,}
π
/
2
−
A
,
{\displaystyle \pi /2-A,}
b
)
{\displaystyle b)}
Pentagramma mirificum (łac. cudowny pentagram ) – w geometrii sferycznej wielokąt gwiaździsty złożony z pięciu łuków kół wielkich , którego wszystkie kąty wewnętrzne są proste . Figurę tę opisał John Napier w pracy Mirifici Logarithmorum Canonis Descriptio (Opis cudownej tabeli logarytmów ) z roku 1614 wraz z regułą Nepera , która wiąże wartości funkcji trygonometrycznych pięciu części trójkąta sferycznego prostokątnego (dwóch kątów i trzech boków). Własności pentagramma mirificum badał między innymi Carl Friedrich Gauss [1]
Na sferze miarą kąta wyraża się zarówno kąty, jak i boki trójkątów sferycznych (łuki kół wielkich). Kąty
A
,
{\displaystyle A,}
B
,
{\displaystyle B,}
C
,
{\displaystyle C,}
D
{\displaystyle D}
E
{\displaystyle E}
P
C
,
{\displaystyle PC,}
P
E
,
{\displaystyle PE,}
Q
D
,
{\displaystyle QD,}
Q
A
,
{\displaystyle QA,}
R
E
,
{\displaystyle RE,}
R
B
,
{\displaystyle RB,}
S
A
,
{\displaystyle SA,}
S
C
,
{\displaystyle SC,}
T
B
{\displaystyle TB}
T
D
{\displaystyle TD}
π
/
2.
{\displaystyle \pi /2.}
P
Q
R
S
T
{\displaystyle PQRST}
P
{\displaystyle P}
R
S
,
{\displaystyle RS,}
Q
{\displaystyle Q}
S
T
{\displaystyle ST}
[2] kąta zewnętrznego przy każdym wierzchołku pięciokąta
P
Q
R
S
T
{\displaystyle PQRST}
∠
A
P
T
=
∠
B
P
Q
=
R
S
⌢
,
{\displaystyle \angle APT=\angle BPQ={\overset {\frown }{RS}},}
∠
B
Q
P
=
∠
C
Q
R
=
S
T
⌢
{\displaystyle \angle BQP=\angle CQR={\overset {\frown }{ST}}}
Koła Nepera trójkątów
A
P
T
,
{\displaystyle APT,}
B
Q
P
,
{\displaystyle BQP,}
C
R
Q
,
{\displaystyle CRQ,}
D
S
R
{\displaystyle DSR}
E
T
S
{\displaystyle ETS}
Gauss wprowadził oznaczenia
(
α
,
β
,
γ
,
δ
,
ε
)
=
(
tg
2
T
P
,
tg
2
P
Q
,
tg
2
Q
R
,
tg
2
R
S
,
tg
2
S
T
)
.
{\displaystyle (\alpha ,\beta ,\gamma ,\delta ,\varepsilon )=(\operatorname {tg} ^{2}TP,\operatorname {tg} ^{2}PQ,\operatorname {tg} ^{2}QR,\operatorname {tg} ^{2}RS,\operatorname {tg} ^{2}ST).}
Zachodzą następujące tożsamości, które pozwalają na wyznaczenie dowolnych trzech z powyższych wielkości na podstawie dwóch pozostałych[3]
1
+
α
=
γ
δ
,
{\displaystyle 1+\alpha =\gamma \delta ,}
1
+
β
=
δ
ϵ
,
{\displaystyle 1+\beta =\delta \epsilon ,}
1
+
γ
=
ϵ
α
,
{\displaystyle 1+\gamma =\epsilon \alpha ,}
1
+
δ
=
α
β
,
{\displaystyle 1+\delta =\alpha \beta ,}
1
+
ϵ
=
β
γ
.
{\displaystyle 1+\epsilon =\beta \gamma .}
Gauss udowodnił następującą „piękną równość” (schöne Gleichung )[3]
3
+
α
+
β
+
γ
+
δ
+
ε
=
α
β
γ
δ
ε
=
(
1
+
α
)
(
1
+
β
)
(
1
+
γ
)
(
1
+
δ
)
(
1
+
ε
)
.
{\displaystyle 3+\alpha +\beta +\gamma +\delta +\varepsilon =\alpha \beta \gamma \delta \varepsilon ={\sqrt {(1+\alpha )(1+\beta )(1+\gamma )(1+\delta )(1+\varepsilon )}}.}
Spełniają ją na przykład liczby
(
α
,
β
,
γ
,
δ
,
ε
)
=
(
9
,
2
/
3
,
2
,
5
,
1
/
3
)
,
{\displaystyle (\alpha ,\beta ,\gamma ,\delta ,\varepsilon )=(9,2/3,2,5,1/3),}
α
β
γ
δ
ε
{\displaystyle \alpha \beta \gamma \delta \varepsilon }
20.
{\displaystyle 20.}
Dowód pierwszej części równości:
α
β
γ
δ
ε
{\displaystyle \alpha \beta \gamma \delta \varepsilon }
=
α
β
γ
(
1
+
α
γ
)
(
1
+
γ
α
)
{\displaystyle {}=\alpha \beta \gamma \left({\frac {1+\alpha }{\gamma }}\right)\left({\frac {1+\gamma }{\alpha }}\right)}
=
β
+
α
β
+
β
γ
+
α
β
γ
{\displaystyle {}=\beta +\alpha \beta +\beta \gamma +\alpha \beta \gamma }
=
β
+
1
+
δ
+
1
+
ε
+
α
(
1
+
ε
)
{\displaystyle {}=\beta +1+\delta +1+\varepsilon +\alpha (1+\varepsilon )}
=
2
+
α
+
β
+
δ
+
ε
+
1
+
γ
{\displaystyle {}=2+\alpha +\beta +\delta +\varepsilon +1+\gamma }
=
3
+
α
+
β
+
γ
+
δ
+
ε
{\displaystyle {}=3+\alpha +\beta +\gamma +\delta +\varepsilon \quad {}}
Dowód drugiej części równości:
(
1
+
α
)
(
1
+
β
)
(
1
+
γ
)
(
1
+
δ
)
(
1
+
ε
)
{\displaystyle {\sqrt {(1+\alpha )(1+\beta )(1+\gamma )(1+\delta )(1+\varepsilon )}}}
=
α
β
⋅
β
γ
⋅
γ
δ
⋅
δ
ε
⋅
ε
α
{\displaystyle {}={\sqrt {\!^{^{^{\!}}}\alpha \beta \cdot \beta \gamma \cdot \gamma \delta \cdot \delta \varepsilon \cdot \varepsilon \alpha }}}
=
α
2
β
2
γ
2
δ
2
ε
2
{\displaystyle {}={\sqrt {\alpha ^{2}\beta ^{2}\gamma ^{2}\delta ^{2}\varepsilon ^{2}}}}
=
α
β
γ
δ
ε
{\displaystyle {}=\alpha \beta \gamma \delta \varepsilon \quad {}}
Również od Gaussa[3]
(
1
+
i
α
)
(
1
+
i
β
)
(
1
+
i
γ
)
(
1
+
i
δ
)
(
1
+
i
ε
)
=
α
β
γ
δ
ε
e
i
S
P
Q
R
S
T
,
{\displaystyle (1+i{\sqrt {\!^{^{\!}}\alpha }})(1+i{\sqrt {\beta }})(1+i{\sqrt {\!^{^{\!}}\gamma }})(1+i{\sqrt {\delta }})(1+i{\sqrt {\!^{^{\!}}\varepsilon }})=\alpha \beta \gamma \delta \varepsilon e^{iS_{PQRST}},}
gdzie
S
P
Q
R
S
T
=
2
π
−
(
|
P
Q
⌢
|
+
|
Q
R
⌢
|
+
|
R
S
⌢
|
+
|
S
T
⌢
|
+
|
T
P
⌢
|
)
{\displaystyle S_{PQRST}=2\pi -(|{\overset {\frown }{PQ}}|+|{\overset {\frown }{QR}}|+|{\overset {\frown }{RS}}|+|{\overset {\frown }{ST}}|+|{\overset {\frown }{TP}}|)}
P
Q
R
S
T
.
{\displaystyle PQRST.}
Obrazem pięciokąta sferycznego
P
Q
R
S
T
{\displaystyle PQRST}
rzucie gnomonicznym (rzucie o środku w środku sfery) na dowolną płaszczyznę styczną do sfery jest pięciokąt prostoliniowy. Jak wiadomo, przez jego pięć wierzchołków
P
′
Q
′
R
′
S
′
T
′
{\displaystyle P'Q'R'S'T'}
krzywa stożkowa ; w tym wypadku jest to elipsa . Gauss wykazał, że wysokości pięciokąta
P
′
Q
′
R
′
S
′
T
′
{\displaystyle P'Q'R'S'T'}
O
′
,
{\displaystyle O',}
[4]
Arthur Cayley zauważył, że jeśli obrać środek układu współrzędnych kartezjańskich w punkcie
O
′
,
{\displaystyle O',}
P
′
Q
′
R
′
S
′
T
′
:
{\displaystyle P'Q'R'S'T'{:}}
(
x
1
,
y
1
)
,
…
,
(
x
5
,
y
5
)
{\displaystyle (x_{1},y_{1}),\dots ,(x_{5},y_{5})}
x
1
x
4
+
y
1
y
4
{\displaystyle x_{1}x_{4}+y_{1}y_{4}}
=
x
2
x
5
+
y
2
y
5
{\displaystyle {}=x_{2}x_{5}+y_{2}y_{5}}
=
x
3
x
1
+
y
3
y
1
{\displaystyle {}=x_{3}x_{1}+y_{3}y_{1}}
=
x
4
x
2
+
y
4
y
2
{\displaystyle {}=x_{4}x_{2}+y_{4}y_{2}}
=
x
5
x
3
+
y
5
y
3
=
−
ϱ
2
,
{\displaystyle {}=x_{5}x_{3}+y_{5}y_{3}=-\varrho ^{2},}
ϱ
{\displaystyle \varrho }
[5]
↑ Pentagramma mirificum . W: Carl Friedrich Gauss: Carl Friedrich Gauss Werke: Band III. Analysis . Königliche Gesellschaft der Wissenschaften zu Göttingen, 1866, s. 481–490.↑ Bruce Director. From Plato’s Theaetetus to Gauss’s Pentagramma Mirificum: A Fight for Truth ↑ a b c H.S.M. Coxeter. Frieze patterns ↑ Bruce Director: On the 375th Anniversary of Kepler’s Passing . [dostęp 2018-12-25]. ↑ Professor Cayley F.R.S. On Gauss’s pentagramma mirificumDOI : 10.1080/14786447108640572 .